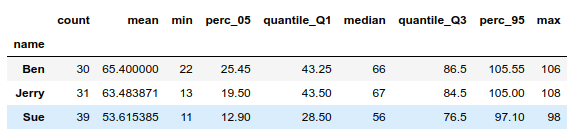
Something I use very often in pandas is named aggregates in groupby’s, but I keep forgetting the somewhat strange syntax, so below is an example. I am aware that one could have used described and percentiles to do much of the same, the lambdas could also be replaced by other more interesting functions.
import pandas as pd import numpy as np # Make a fake dataframe ages = np.random.randint(low=10, high=110, size=100) names = np.random.choice(['Ben', 'Jerry', 'Sue'], size=100) df = pd.DataFrame(list(zip(names, ages)), columns = ['name', 'age']) # Group and calculate aggregates df.groupby(['name']).agg( count = ('age', 'count'), mean = ('age', 'mean'), #mode = ('age', pd.Series.mode), min = ('age', 'min'), perc_05 = ('age', lambda x: x.quantile(0.05)), quantile_Q1 = ('age', lambda x: x.quantile(0.25)), median = ('age', 'median'), quantile_Q3 = ('age', lambda x: x.quantile(0.75)), perc_95 = ('age', lambda x: x.quantile(0.95)), max = ('age', 'max'), )