Enhancing pandas groupby with bootstrapped confidence intervals

import pandas as pd
import seaborn as sns
import tqdm
import random
from datetime import datetime
import tqdm
import numpy as np
from scipy.stats import sem
from sklearn.utils import resample
import matplotlib.pyplot as plt
sns.set_style("darkgrid")
 
# Create a mock dataframe with two categorical columns and one scoring column
random.seed(42)
num_rows = 3500
 
data = {
    "A": [random.choice(["lorem", "ipsum", "dolor"]) for _ in range(num_rows)],
    "B": [random.choice(["foo", "bar"]) for _ in range(num_rows)],
    "score": [random.randint(1, 5) for _ in range(num_rows)],
}
df = pd.DataFrame(data)
df.head()

A   B   score
0   dolor   foo 5
1   lorem   bar 3
2   lorem   bar 2
3   dolor   bar 2
4   ipsum   foo 2

def calc_mean_count_ci(_df, groupby_cols=None, stat_col=None, n_bootstrap=1000, save_to_file=False):
    """
    Calculate mean, count, and confidence intervals using bootstrapping.
 
    Parameters:
    - _df (DataFrame): Input DataFrame containing the data.
    - groupby_cols (list, optional): List of columns to group the data by. Default is None.
    - stat_col (str, optional): Column name for which to calculate mean, count, and confidence intervals.
    - n_bootstrap (int, optional): Number of bootstrap samples to generate. Default is 1000.
    - save_to_file (bool, optional): If True, save the results to a CSV file. Default is False.
 
    Returns:
    - DataFrame: A DataFrame containing mean, count, and confidence interval information
                 for the specified groupby columns and statistical column.
 
    Example:
    >>> result_df = calc_mean_count_ci(df, ['A', 'B'], 'score')
 
    Notes:
    - The function utilizes bootstrapping to estimate the confidence interval for the mean.
    - The result DataFrame includes columns for count, mean, and confidence intervals.
    - If save_to_file is True, the result is saved to a CSV file with a filename based on the current date,
      groupby columns, statistical column, and the term 'mean_count_ci'.
    """
 
    # Define a function to calculate confidence interval using bootstrapping
    def calculate_ci_bootstrap(data):
        means = []
        for _ in range(n_bootstrap):
            sample = resample(data)  # Bootstrap resampling
            mean = np.mean(sample)  # Calculate mean of the resampled data
            means.append(mean)
 
        # Calculate the mean of the whole dataset and the confidence interval 
        # from the distribution of the sample means
        data_mean = np.mean(data)
        confidence_interval = np.percentile(means, [2.5, 97.5])
 
        return pd.DataFrame({
            'count': [len(data)],
            'mean_ci_lower': [confidence_interval[0]],
            'mean': [data_mean],
            'mean_ci_upper': [confidence_interval[1]],
        }).round(4)
 
    # Group by columns A and B, apply the calculate_ci_bootstrap function to 
    # the 'score' column, and merge the results
    result = (
        _df.groupby(groupby_cols)[stat_col]
        .apply(calculate_ci_bootstrap)
        .reset_index()
        .drop(columns=["level_2"])
    )
 
    # Save the data to a file with the current date, columns and basic info the dataframe
    if save_to_file:
        name = f'{datetime.now().date().isoformat()}-{"-".join(groupby_cols)}-{stat_col}-mean_count_ci.csv'
        result.to_csv(name, index=False)
        print(f'Saved data to {name}')
 
    return result
 
calc_mean_count_ci(df, ['A', 'B'], 'score')

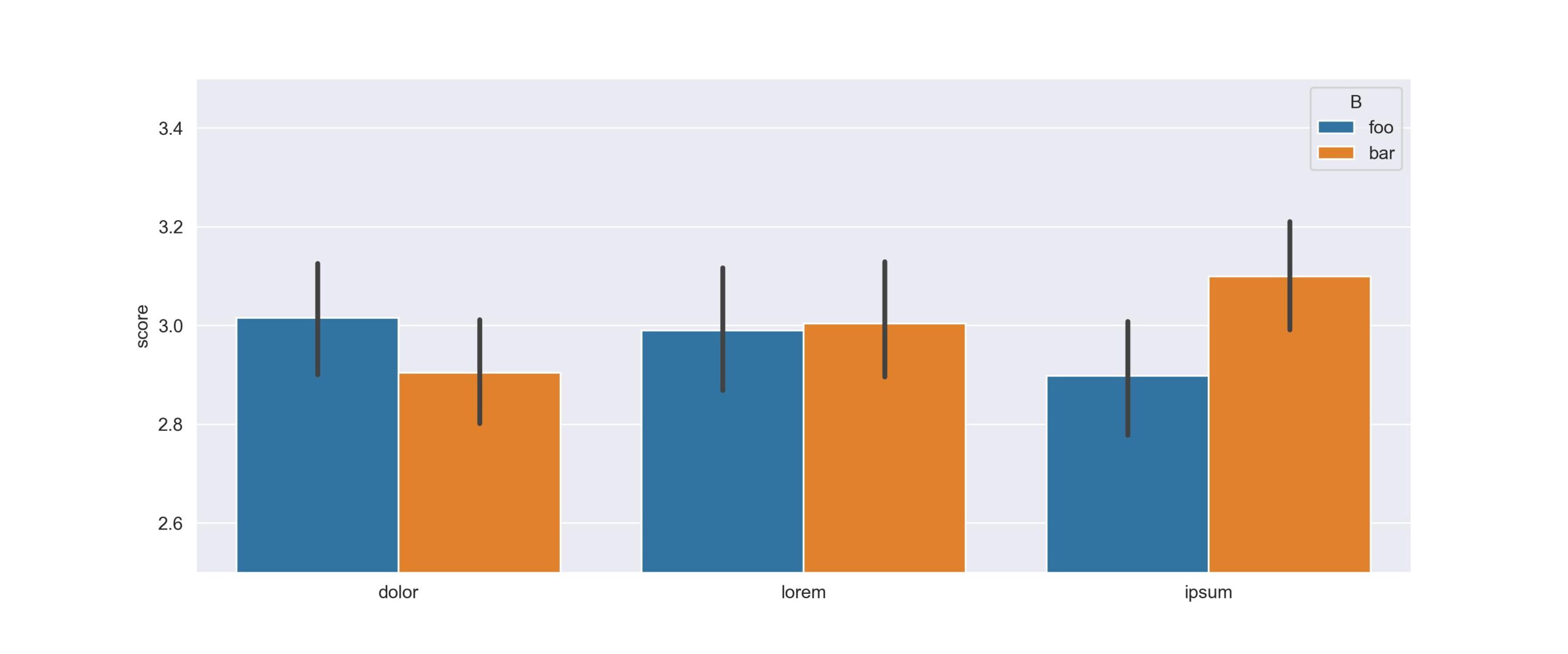
A   B   count   mean_ci_lower   mean    mean_ci_upper
0   dolor   bar 605 2.7933  2.9041  3.0117
1   dolor   foo 591 2.8967  3.0152  3.1286
2   ipsum   bar 584 2.9829  3.0993  3.2072
3   ipsum   foo 608 2.7878  2.8980  3.0066
4   lorem   bar 548 2.8814  3.0036  3.1241
5   lorem   foo 564 2.8741  2.9894  3.1046

fig, ax = plt.subplots(figsize=(12, 5))
sns.barplot(data=df, y="score", x="A", hue="B", ax=ax)
ax.set_xlabel("")
ax.set_ylim([2.5, 3.5])
plt.savefig(f"bootstrap_example_dataset_size_{num_rows}.jpg", dpi=300)